paradoxes d’Achille et la tortue : Réfutation de la prétendue résolution mathématique
Version 7 du 10.4.2024
De nos jours, une croyance largement répandue prétend que les paradoxes de Zénon ont été résolus grâce au calcul infinitésimal. Cette idée gagne en crédibilité du fait de sa large diffusion, notamment sur des plateformes comme Wikipédia.
La solution habituellement proposée prétend qu'Achille rattraperait la tortue en cumulant une série infinie de segments qui, malgré leur nombre illimité, convergeraient vers un total fini, suggérant ainsi une erreur de Zénon. Cependant, cette interprétation, bien que mathématiquement valide, néglige un aspect fondamental de cette méthode mathématique : la convergence. Dans cet article, je vais souligner l'importance de cette notion souvent omise, essentielle pour une compréhension véritable du temps. Loin de contredire Zénon, le calcul infinitésimal souligne la validité de son argument. Je démontrerai comment la convergence confirme la justesse de Zénon et pourquoi, au lieu de résoudre le paradoxe, le calcul infinitésimal se prête parfaitement à sa reformulation mathématique. Le calcul infinitésimal met en lumière la complexité des paradoxes de Zénon, affirmant leur pertinence et actualité.
La limite et la convergence deux notion à savoir distinguer:
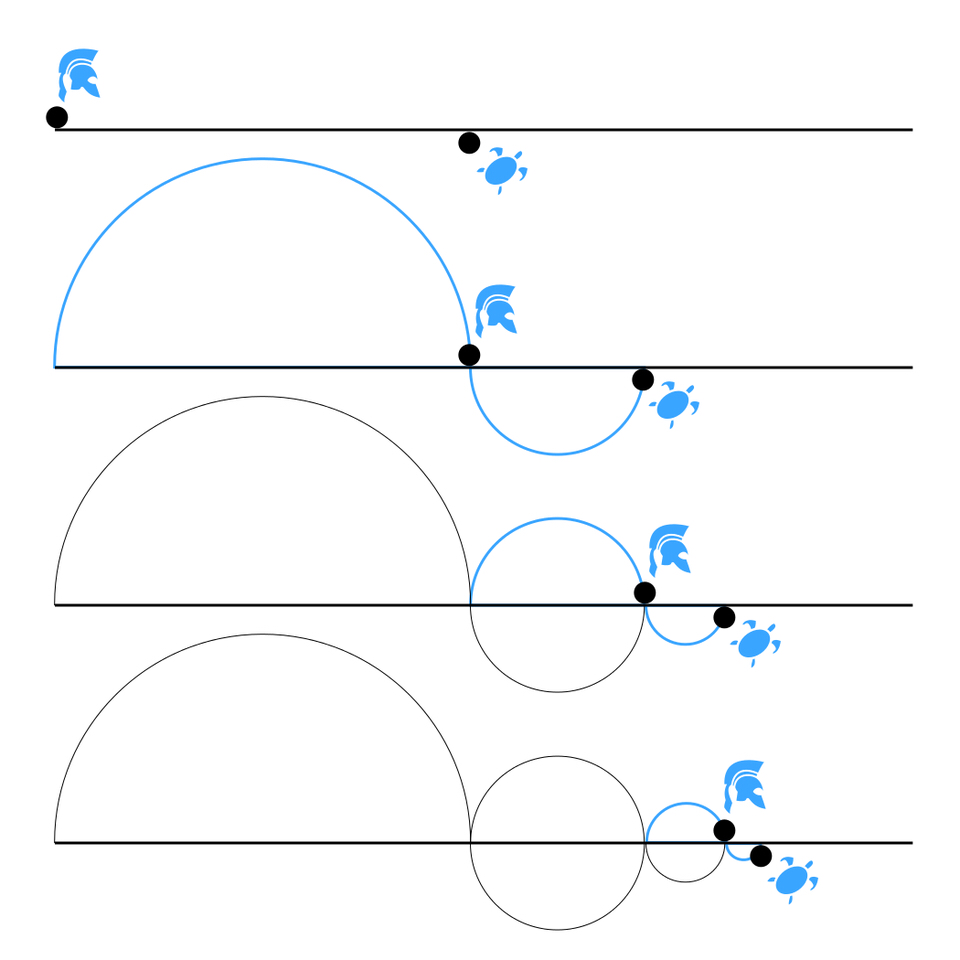
Dans le paradoxe d'Achille et la tortue, le calcul infinitésimal nous parle de deux choses qui s’opposent et qui ne doivent pas être confondues : la limite et la convergence. Lorsqu’on parle de convergence, on se réfère au processus selon lequel la somme des termes d’une série s’approche d’une valeur limite, sans jamais la dépasser, peu importe le nombre de termes ajoutés.
Cette notion est illustrée par l’effort d’Achille pour rattraper la tortue, où chaque étape le rapproche de son objectif, mais introduit simultanément une nouvelle étape à franchir.
Imaginons Achille qui court deux fois plus vite que la tortue et essaie de rattraper un retard de 20 secondes. Il arrive en position "B" là où était la tortue en 10 secondes. Mais pendant ce temps, la tortue a bougé en "C". À chaque fois qu'Achille arrive là où était la tortue, il doit encore courir un peu plus, parce que la tortue a encore avancé entretemps. Lorsqu’Achille réalise qu'après avoir parcouru un bout de chemin, il lui reste toujours 10 secondes, puis 5, 2.5, 1.25, etc., il découvre que ce voyage continue sans conclusion finale, car dans l’épreuve du temps, il existe toujours de nouveaux termes à ajouter, et cette addition ne finit jamais, contrairement à la limite qui, elle, est fixe.
C'est ça, la convergence. Achille se retrouve face à un infini, mais un infini qui se dévoile non pas en s'étendant dans la longueur, mais en se réduisant à l'extrême, dans l'ultracourt. Il se retrouve face à une éternité dans l'espace et le temps, mais un infini et une éternité qui se dévoilent non pas en s'étendant dans la longueur, mais en occupant un parcours parfaitement fini ; un infini dans le fini, d’où l’immense intrigue et donc, le paradoxe.
L'erreur serait de penser que, parce que ces distances deviennent infiniment petites, elles pourraient devenir négligeables et que l’on pourrait les oublier d’un revers de main. Mais c'est un biais cognitif : ces parcours, bien qu'infiniment courts, sont bel et bien là, et omettre ne serait-ce qu'une seule de ces étapes serait comme omettre les dernières pièces d’un puzzle en prétendant que, parce qu’il est presque fini en apparence, c’est qu’il l’est entièrement.
La notion de la limite en calcul infinitésimal comparée à un puzzle :
Le trajet d’Achille est comme un puzzle qui aurait un nombre infini de pièces, une succession de mouvements devenant de plus en plus petits restant pour Achille. La limite permet de calculer la taille finale du puzzle, comme si ce puzzle était déjà fini. Elle ne se préoccupe pas de comment cette finitude est atteinte dans l’épreuve du temps, ni de la raison de cette possibilité. Elle constate juste que le parcours est fini après 20 secondes ; Achille dépasse sa rivale. C’est un constat, un calcul correct, mais il est en revanche parfaitement incapable d’expliquer pourquoi et comment cette finitude a été rendue possible et comment il est possible de construire un puzzle pièce par pièce dans un ordre chronologique sans fin sans jamais trouver de pièce finale et dans un temps fini.
Tant que cela n’est pas expliqué, la limite ne peut ni comprendre ni expliquer le pourquoi du comment ; elle ne fait que constater qu’après 20 secondes, le puzzle s’est terminé, mais est parfaitement incapable d’expliquer comment ni pourquoi cette réalisation est possible. La limite ne résout pas la problématique de Zénon; elle ne fait que constater le dépassement d’Achille, ce que quiconque peut aisément faire sans avoir recours à des mathématiques compliqués.
La convergence : placer les pièces du puzzle dans un ordre précis
Le paradoxe de Zénon ne se résume pas à trouver la taille du cadre en calculant juste la limite. Pour saisir pleinement l'immense problématique soulevée par Zénon, il s'agit de comprendre comment chaque pièce du puzzle, représentant les étapes qu’Achille doit franchir, s'insère dans ce cadre au fil du temps. La convergence illustre ce processus, montrant comment Achille se rapproche progressivement de la tortue, une pièce à la fois, dans un ordre chronologique strict — "A", "B", "C" — qui doit être scrupuleusement respecté. Chaque étape franchie par Achille est comme une pièce du puzzle se mettant en place, une à une, dans un ordre chronologique ininterrompu. Pourtant, ce processus soulève un problème majeur : puisque le nombre de pièces est infini et qu'il faut un temps non nul pour traverser chaque nouveau parcours, même infime, le temps devrait être infini puisqu’il n'y a pas de dernier parcours autrement, il ne pourrait pas être en nombre infini. Ainsi, c'est dans l'épreuve du temps que la convergence révèle la véritable problématique, celle-là même soulevée par Zénon. S'il n’y a pas de dernière pièce au puzzle, comment est-il possible de le finir ?
L'erreur commune d’omettre la convergence
L'erreur commune serait de penser que, puisque le dépassement est effectif par l'observation, on pourrait rejeter la convergence pour ne prendre en compte que la limite, mais c'est une erreur. Car, dans le temps, seule la convergence est capable de reproduire fidèlement l'épreuve du temps. Se contenter de calculer la limite pour présenter l'état du puzzle fini, c’est oublier le facteur de progression temporelle dans lequel le parcours d’Achille doit passer dans un ordre chronologique par des étapes sans en altérer l’ordre, « A », « B », « C », etc., à l’infini. La limite n'explique en rien comment le puzzle peut être finalisé malgré l'absence de dernière pièce.
Ainsi, loin de résoudre le paradoxe, le calcul infinitésimal le reproduit fidèlement. D'une part, la convergence pose la question de comment la limite peut être atteinte et, d'autre part, elle s’oppose directement à l’atteinte de cette limite. Bien que la convergence permette de situer où doit se trouver la limite, ni la convergence ni la limite ne peuvent expliquer comment le puzzle peut être achevé et donc résoudre l’intrigue millénaire de Zénon.
La limite indique où le puzzle sera fini, mais la convergence montre que l'atteinte de cette limite n'est mathématiquement pas réalisable, reproduisant ainsi très fidèlement le problème soulevé par Zénon. En effet, dans le calcul infinitésimal, la convergence n’atteint jamais la limite et se contente de s’en approcher indéfiniment, reflétant ainsi très fidèlement le paradoxe de Zénon, ce qui est également le cas avec le paradoxe de la dichotomie. Il est incorrect de croire que le calcul infinitésimal pourrait résoudre l'équation; cette idée est un paralogisme où seule la limite a été prise en compte et la convergence omise.
En conclusion, l'exploration du paradoxe à travers l'analogie du puzzle nous enseigne que la question véritable n'est pas de savoir si Achille dépasse la tortue, puisqu'elle est dépassée, mais plutôt comment ce dépassement est rendu possible. La limite est parfaitement incapable d’expliquer comment ni pourquoi cette réalisation est possible. La limite ne résout pas la problématique de Zénon; celle-ci est mise en évidence par la convergence et non par la limite.
Recherche personnel :
Depuis 1998, je développe des théories sur l'espace-temps pour explorer, entre autres, des paradoxes tels que ceux de Zénon d'une manière inédite. La plus convaincante à mon sens, la Tranche Minimum de Perception Temporelle (TMPT), postule que notre perception du temps est limitée et ne s'active qu'au-delà d'une durée minimale.
Tout comme les images d'un film créent l'illusion du mouvement alors que la bobine est immobile, nos TMPT façonnent notre perception de la continuité temporelle.Sur mon site, je détaille le cheminement de mes réflexions et les raisons pour lesquelles ces idées me semblent particulièrement pertinentes.
Je soutiens que l'univers s'étend au-delà de nos TMPT dans un monde parallèle qui échappe à notre perception, où l'infini constituerait la cinquième dimension de l'univers et l'éternité, la 6e dimension. Sans la compréhension de ces dimensions supplémentaires, il est tout à fait logique de percevoir des contradictions dans les paradoxes de Zénon. Ces contradictions émergent parce que nos sens ne nous révèlent pas la réalité du mouvement dans ces réalité parallèles invisibles à nos sens.
Mon livre numérique gratuit explore ces idées et propose une nouvelle voie pour appréhender ces énigmes antiques. Je vous invite à rejoindre la discussion et à partager vos réflexions via les commentaires sur Facebook, accessibles depuis chaque article de mon site.Cet article, issu de mes recherches, est libre d'utilisation, à condition de mentionner la source.
Olivier Dusong
